Основи математичної фізики
Основи математичної фізики
[ред.]Математична фізика належить до прикладної математики, взагалом, диференціальних рівнянь (коректно поставлена задача за Адамаром, крайові задачі, асимптотичні методи, топологічна, метрична ентропія тощо). Тобто математична фізика не належить до теоретичної математики. Щоб краще зрозуміти з'ясувати зв'язок між фізикою та математикою, звернімося до словника. Відомий математик Ю.І.Манін пояснює математику як метафору (грец. μεταφορά — "перенесення" від μετά "над" + φορός "несучий"). Префікс "мета-" (грец. μέτα) — грецький прийменник та відповідний префікс, що означає "з" (у місці), "посеред", "після" (у часі), а також "поряд" та "понад" (у переносному значенні, як у слові метафора). Як говорилося раніше, алгебра вивчає час, геометрія вивчає простір, а аналіз - континуум час-простір. Поняття математичної фізики можна ототожнити із поняттям метафізики (грец. Τά μετά τά φυσικά — "те, що понад фізикою"). Таким чином, термін "математична фізика" є синонімом терміну "метафізика".
Теореми існування розглядаються з інтуїціоністської та з конструктивної точок зору. З конструктивної точки зору ставиться питання про конструктивність (ефективність побудови) об'єкта, існування якого доводиться. Теорема, у якій об'єкт конструюється, вважається більш змістовною, ніж так звана теорема, у якій стверджується існування деякого об'єкта, однак нічого не говориться про те, як він влаштований. За інтуїціоністського підходу теореми існування формулюються більш слабко, ніж за конструктивного. Теореми першого типу називаються конструктивними теоремами існування, теоремами другого типу - теоремами чистого існування. Конструктивні теореми доводяться складніше, ніж відповідні теореми чистого існування, або на деякому етапі математичної творчості математиків-теоретиків вони можуть бути невідомими. Фізики використовують математичні об'єкти, винайдені математиками-теоретиками, реалізуючи їх у матеріальних формах. У цьому сенсі діяльність фізиків - це матеріальні демонстрації математичних об'єктів (подібно до того, як група кубіка-рубіка представляється самим предметом - кубіком-рубіка). Наприклад, як у випадку із гомологіями Хованова: можна розглядати функтор між категорією оснащених кобордизмів одновимірних многовидів й категорією ланцюгових комплексів. Така інтерпретація встановлює зв'язок між топологічною квантовою теорією поля й теорією вузлів. Фізики шукають подібні зв'язки, метафорично бавлячись у пісочниці, яку побудували математики. Спільнота фізиків містить й багато аферистів, наприклад, які пропагують так звані часові кристали та їх зв'язок із квантовими комп'ютерами. Самі квантові комп'ютери - це афера, якщо розібратися у фізичному змісті квантової заплутаності (що пов'язана із поняттям ентропії, чи інтрапсихічної атаксії).
З іншого боку, наприкінці 1980-х років Ю.І.Манін помітив, о 1960-ті були 10-річним розквітом для алгебричної топології, 1970-ті - для алгебричної геометрії, 1980-ті - для математичної фізики. У цьому сенсі, математик М.С.Вербицький вважає, що 1980-ті тривають до цих пір, оскільки математичні ідеї, пов'язані із 1990-ми (гіпотеза Концевича, інваріанти Громова-Уїттена, інваріанти Зайберга-Уїттена, квантові когомології) - усі походять з теорії струн. Математика втратила загальний контекст, а в умовах втрати абстрактних чинників єдиним ефективним чинником стає утилітарний: математика лише тому цікава, що вона пов'язана із теорією струн (майже уся математика, яка відноситься до фізики, відноситься до струнної геометрії). Релевантність для фізики - це єдиний чинник, усі цікаві ідеї зазвичай пов'язані із фізикою струн.
Говорячи про фізичне товариство, необхідно відзначити, що вже давно існує мода на присвоєння певним математичним об'єктам, ідеям імен людей. Такий підхід натякає на потенційну можливість уведення права на власність. Скажімо, відомий фізик Альберт Ейнштейн за заповітом передав Єврейському університету свої особисті й наукові праці (в наслідок чого були організовані університетські Архіви Альберта Ейнштейна). Щоб запобігти привласненню математичних об'єктів та ідей, бажано відмовитися від такого підходу, надавати перевагу абревіатурам (за фразеологізмом "називати речі своїми іменами").
З'ясування суті фізичного простору-часу відноситься до числа найважливіших питань фундаментальної фізики й усього природознавства в цілому. Погляди на суть простору і часу базуються на двох підходах: субстанціальному й реляційному. Реляційний підхід базується на понятті відношення (лат. relativus - відносний). Наприклад, у геометрії відношенням є метрика (відстані). У сучасній геометрії спочатку розглядають координатну систему у многовиді певної розмірності, а згодом задається метрика. Однак можна мислити й навпаки: можна починати із відстаней (парних відношень між точками), а потім вже з них отримувати координати й усі інші поняття.
Реляційний підхід називають також концепцією дальнодії, згідно до якої тіла діють один на одного без матеріальних посередників, через пустоту, на будь-якій відстані. Субстанціалізм називають також концепцією близькодії, згідно до якої взаємодії передаються за допомогою матеріальних посередників та із скінченною швидкістю (наприклад, у випадку електромагнітних взаємодій таким посередником є електромагнітне поле, яке розповсюджується із швидкістю світла).
У найпростішій математичній моделі реляційної фізики розглядають множину елементів довільної природи, між якими визначені (числові) відношення, наділені певними алгебричними властивостями. У математичному сенсі елемент множини є примітивом теорії, тобто це поняття є вихідним. У фізичному ж сенсі в якості елементів можуть бути геометричні точки, точки-події теорії відносності, фізичні тіла, елементарні частинки тощо. В загальному випадку відношення між елементами - це комплексне або дійсне число, яке ставиться у відповідність парі, трійці, четвірці тощо елементів, які належать до однієї чи різних множин. В якості відношень можуть розглядатися відстані між точками, метрика, скалярні добутки векторів тощо. Найбільш важливими є випадки, коли числа ставляться у відповідність парам елементів - саме такими є метричні відношення у загальноприйнятій геометрії або теорії афінних просторів.
В цілому, математику умовно ділять на лінгвістичну (дискретну) й неперервну (фізичну). Математична фізика досліджує процеси у системі, яка зазвичай представляє собою декотру область простору, заповнену неперервним матеріальним середовищем (суцільним середовищем). У цій області величини, які описують становище середовища й процеси, які у ньому відбуваються, залежать від просторових координат та часу. Теоретичною основою для побудови математичних моделей процесів у таких областях є механіка та електродинаміка неперервних (суцільних) середовищ. У загальному, у математичній фізиці розглядають 3 рівня поведінки системи:
- взаємодія системи із суцільним середовищем;
- взаємодія елементарних об'ємів системи;
- властивості окремо взятого елементарного об'єму.
На першому рівні взаємодія розглядається з точки зору так званих крайових умов, тобто умов на межі області рішення задачі. Ці умови містять так звані граничні й початкові умови. На другому рівні описується взаємодія елементарних об'ємів на засадах законів збереження фізичних субстанцій та їх переміщення у просторі, що дозволяє розглядати моделі процесів перенесення цих субстанцій. На третьому рівні віднаходяться рівняння стану середовища, тобто будуються моделі поведінки середовища у елементарному об'ємі.
Для задач фізичної природи висуваються такі вимоги:
- існування розв'язку; задача повинна мати розв'язок (задача яка має розв'язок не представляє інтересу як математична модель);
- єдиність розв'язку; не повинно існувати декілька розв'язків задачі;
- неперервна залежність від вхідних даних; розв'язок задачі повинен мало змінюватись при малій зміні вхідних даних.
Фізичні величини
[ред.]Найпростішим поняттям математики є поняття числа. Людина сприймає предмети або роздільно існуючі, або у їх сукупності (стадо тварин, купка валунів тощо). Поняття одиниці та поняття множини одиниць є суперечливими. Поняття числа включає у себе і поняття множини, і поняття одиниць, що її складають. За Евклідом число є множиною одиниць.
До 19 століття важалося, що математика є несуперечливою, однак згодом неочікувано виникли труднощі, які вказували на необхідність глибокого аналізу основ. У книзі "Principia Mathematica" Уайтхед та Расел показали, що математичні твердження про дійсні числа (і не лише про відношення цілих чисел, як додатних, так й від'ємних) можна сформулювати по-іншому: як уявлення про елементарну відповідність класів (яка встановлюється співставленням їх елементів), так що їх можна вивести із аксіом такого співставлення й аксіом чистої логіки. Число є властивістю, спільною для усіх класів, які можуть бути поставлені один одному у відповідність шляхом співставлення їх елементів (по одному з кожного класу), відтак усі елементи утворюють пари і жодного зайвого не залишається.
Використання математики - це використання мови, за допомогою якої можна встановлювати співвідношення, надто складні для того, щоб їх можна було достатньо коротко описати природною мовою. Правила, яким підпорядковуються символи - граматика такої мови. Для того, щоб бути придатною, мова повинна задовільняти двом умовам:
- з її допомогою можна сказати, що потрібно (тобто вона має бути достатньо загальною);
- вона повинна бути несуперечливою.
К.Ґьодель та Р.Карнап показали, що несуперечливість системи математичних аксіом не може бути доказаною методами, які базуються лише на правилах даної системи.
У фізиці фундаментальне поняття виміру є близьким до поняття додавання, а більшість фізичних законів за своєю суттю є твердженнями про пропорційності, що відповідає поняттям множення та ділення. Величини, які можна виміряти за допомогою фізичного додавання, називаються елементарними (основними величинами). Найбільш важливими серед них є числа (класів), довжина, час та маса.
Елементи системи утворюють поле якщо:
1) та є однозначно визначеними елементами для будь-яких
2) (справджується переставний закон додавання);
3) (справджується сполучний закон додавання);
4) (справджується переставний закон множення);
5) (справджується сполучний закон множення);
6) (справджується розподільний закон множення);
7) поле містить два елементи та такі, що та для будь-якого ( - ідемпотент або одиниця поля , тобто );
8) для будь-якого елемента існує елемент такий, що ;
9) для кожного елемента окрім елемента (нуля), існує протилежний елемент такий, що (тобто ).
Перші сім правил справджуються, якщо поле складається лише з додатних цілих чисел із нулем, . Останні два правила не справедливі для такого поля, оскільки у такому немає такого цілого що за і немає такого цілого за якого якщо вважати Восьме правило уводить від'ємні числа та, відповідно, віднімання. Дев'яте правило уводить зворотні величини (і звідси ділення та раціональні дроби). Ці правила справджуються, якщо поле складається з усіх раціональних чисел (додатних та від'ємних). Сформульовані правила не встановлюють яке-небудь відношення порядку, тобто хоча вони матьна увазі поняття рівності (та, відповідно, нерівності ), вони не уводять поняття "більше" () чи "менше" (). У фізиці вимір є встановленням рівності у межах певної похибки (а не точної рівності), відтак необхідні додаткові правила, які визначають нерівності:
10) для будь-яких справджуються та якщо (закон порівнюваності);
11) для опціонально справджується лише одне: чи чи чи (трихотомія);
12) якщо та то (властивість транзитивності);
13) якщо тоді для довільного (адитивність впорядкування);
14) якщо та то (мультиплікативність впорякування);
15) якщо то (визначення знаку ).
Якщо застосувати до поняття фізичної величини алгебру, то виникне запитання про зміст виразів та якщо - довжина, а - час чи маса. Можна інтерпретувати специфічним чином суму однак рівності не можна надати жодного фізичного змісту. Навпаки, вираз буде означати відповідно швидкість або довжину на одиницю маси. Відтак правила 10-14 потребують виправлення: оскільки усі числа є порівнюваними, то мова не виражала би той факт, що безглуздо говорити, що, наприклад, час є більшим від щільності. До трьох можливостей, передбачених правилом 10, необхідно додати четверту: та можуть бути непорівнюваними та, відповідно, належати різним полям, а їх добуток та відношення, у свою чергу, можуть належати іншим полям. Таким чином, поле усіх фізичних величин розбивається на класи: величини, які належать до одного класу, є порівнюваними між собою, але їх добуток належить до іншого класу лише якщо один із співмножників не є числом. У цьому сенсі мова, необхідна для фізики, не цілком співпадає із звичайною алгеброю. Величини різних розмірностей є непорівнюваними; непорівнюваними є також й декотрі величини однакової розмірності. Можна сказати, що поле фізичних величин задовільняє законам алгебри, але із наступним застереженням: порівнювані величини задовільняють умові 10, і їх можна додавати (за виконання обчислень), а непорівнювані не можна.
Математична модель
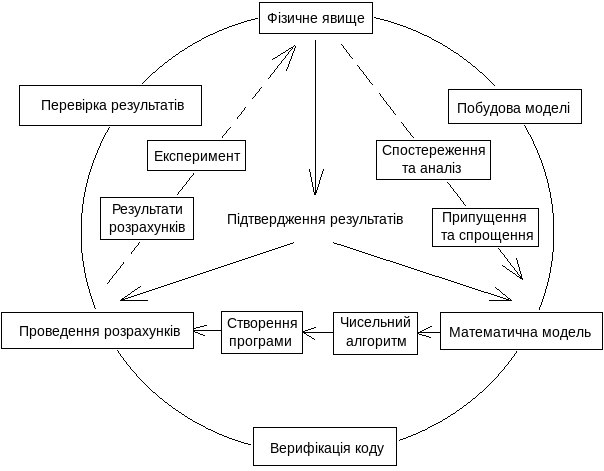
[ред.]За російським академіком А.А.Самарським, "...математична модель - це еквівалент об'єкта, який відбиває у математичній формі найважливіші властивості - закони, яким він підпорядковується, зв'язки, притаманні складовим його частинам тощо". Причому сама постановка задачі про математичне моделювання якого-небудь об'єкта породжує чіткий план дій, який можна розташувати у три етапи:
- модель; обирається "еквівалент" ("математична метафора") об'єкта, який у математичній формі виражає найважливіші його властивості - закони, яким він підпорядковується, зв'язки, притаманні його частинам тощо; математичні моделі досліджуються теоретичними методами;
- алгоритм; розробляється послідовність дій для реалізації моделі на обчислювальній техніці; модель тут представляється у формі, зручній для застосування чисельних методів, визначається послідовність обчислювальних й логічних операцій, які потрібно здійснити, щоб віднайти шукані величини із заданою точністю;
- програма; розробляється програм, яка переводить модель та алгоритм на доступну для обчислювальної техніки мову (так званий електронний еквівалент досліджуваного об'єкта).
- алгоритм; розробляється послідовність дій для реалізації моделі на обчислювальній техніці; модель тут представляється у формі, зручній для застосування чисельних методів, визначається послідовність обчислювальних й логічних операцій, які потрібно здійснити, щоб віднайти шукані величини із заданою точністю;
Описати кількісно яку-небудь ситуацію чи подію - значить для декотрого числа параметрів обраних в якості характеристичних, вказати їх числові значення, які встановлюються при спостереженнях. Дві ситуації (або дві події) є порівнюваними, якщо характеристичні параметри для них будуть однаковими. Два описи, які використовують однакові параметри, називаються рівноцінними. У випадку, коли є число рівноцінних описів порівнюваних ситуацій або подій, можна кожне з них зобразити точкою у -вимірному просторі із параметрами в якості координат. Розподіл цих точок представляє експериментальний матеріал. Якщо відома достатня кількість точок, то такий розподіл можна розглядати як функцію, яка дає щільність розподілу. Якщо множина точок концентрується у просторі меншого числа вимірів то між параметрами існує закономірних співвідношень, відшукання яких складає одну з основних задач фізики. У протилежному випадку відомі лише статистичі співвідношення, які представляються за допомогою функції
Многовиди - множини точок у багатовимірному просторі (множини чисел, які "зануляють" усі рівнння системи). Ці множини наділені структурами, одна з яких, алгебрична, робить їх алгебричними многовидами. Існують й інші структури, наприклад, симплектична, яка має іншу природу, відмінну від алгебричної. Таким чином, множина може мати дві структури, а значить, бути одночасно алгебричним й симплектичним многовидом. Гіпотеза гомологічної дзеркальної симетрії стверджує, що симплектична структура відповідає алгебричній, і навпаки. Ця гіпотеза була підтверджена російським математиком О.І.Ефімовим.
Щільність субстанцій
[ред.]Розгляньмо окіл точки із діаметром та об'ємом Помістимо до масу декотрого суцільного середовища. Границя
називається щільністю (кг/м) середовища у точці простору до якої стягується окіл за
Таким самим чином можна визначити й енергію, зосереджену у деякій області простору, тобто її об'ємну щільність як границю де - кількість енергії (Дж/м), зосередженої у об'ємі Наприклад, при розгляді електричного заряду, тобто у можна говорити про об'ємну щільність електричного заряду (Кл/м):
Позначмо евклідовий простір розмірності через декартові координати точки цього простору позначаються через Область - відкрита множина, що належить евклідовому просторові, яка задовольняє наступним умовам:
- за будь-якого розбиття цієї множини на дві частини хоча б одна з цих частин містить граничну точку іншої частини (умова неперервності евклідового простору, що містить дану множину, частини якої невідокремлювані, тобто зв'язні);
- кожна її точка має окіл.
Наприклад, на площині внутрішність диску є областю, а сукупність внутрішніх точок двох дисків, що торкаються ззовні, які утворюють разом відкриту множину, не є областю. Ще як приклад, областю є довільний інтервал на прямій (за визначенням, ).
Часто доводиться здійснювати інтегрування по множинам різної розмірності, розташованим у просторі зокрема, доводиться інтегрувати по області чи по -вимірній поверхні. Якщо змінна точка інтегрування позначена то елемент міри Лебега ("елемент об'єму") у просторі позначається через диференціал Елемент міри на поверхні ("елемент площі поверхні") позначається через диференціал де через позначається сама поверхня.
Якщо - множина точок простору то замикання цієї множини позначається через Якщо - декотра область у просторі a - її границя, то Підобластю області називається область Підобласть називається внутрішньою, якщо вона разом із своєю границею міститься у тобто
Топологічний векторний простір (над полем дійсних чисел ) - векторний простір із такою топологією, що операції додавання та множення на скаляр є неперервними. Зручно вважати, що простір є гаусдорфовим й локально опуклим. Останнє означає, що кожний окіл нуля містить опуклий окіл нуля, тобто такий відкритий окіл що якщо та то належить Топологічні векторні простори із неперервними лінійними відображеннями (в якості морфізмів) утворюють категорію (під лінійністю розуміється лінійність відносно множення на дійсне число).
Конфігураційний простір
[ред.]Положення елементарної частинки у просторі визначається впорядкованою парою чисел які називаються її координатами у просторі. Множина усіх таких впорядкованих трійок є декартовим кубом трьох числових осей При русі у кожний момент часу частинка знаходиться у декотрій точці простору із координатами Таким чином, рух частинки може пояснюватися як відображення де - вісь часу, а - трьохвимірний простір. Зазвичай вважають тому
Якщо система складається з числа елементарних частинок, то її конфігурація задається положенням кожної із цих частинок, тобто впорядкованим набором з чисел. Множина усіх таких наборів називається конфігураційним простором системи частинок. Таким чином, конфігураційний простір системи частинок можна розуміти як декартів добуток числа екземплярів простору Руху частинок відповідає відображення осі часу до конфігураційного простору системи.
Наприклад, нехай - потенційна енергія механічної системи, що пов'язана із взаємним розташуванням елементарних частинок системи, тобто визначається конфігурацією цієї системи. Нехай - підмножина конфігураційного простору системи. Кожному положенню системи відповідає декотре значення потенційної енергії. Таким чином, потенційна енергія задається функцією що визначена на підмножині конфігураційного простору із значеннями у області дійсних чисел.
Кінетична енергія системи матеріальних частинок залежить від їхніх швидкостей. Повна механічна енергія системи дорівнює тобто сумі кінетичної та потенційної енергій. Повна механічна енергія залежить, таким чином, як від конфігурації системи, так й від набору швидкостей її частинок. Як і конфігурація частинок у просторі, набір що складається із трьохвимірних векторів, може бути заданий впорядкованим набором з чисел. Впорядковані пари що відповідають станам системи, утворюють підмножину у декартовому добутку яка називається фазовим простором системи частинок (на відміну від конфігураційного простору ). Повна енергія системи є функцією що визначена на підмножині фазового простору і яка приймає значення у області дійсних чисел. Зокрема, якщо система замкнута, тобто їх не повідомляється енергія ззовні (якщо на неї не діють зовнішні сили), то за законом збереження енергії у будь-якій точці множини станів системи функція буде мати однакове значення
Група Галілея
[ред.]Властивості перетворення фазового простору визначає властивості динамічної системи, тобто фізику системи. Група перетворень - це множина перетворень яка визначає фізичну картину динаміки і має наступні властивості:
- множина містить тотожне перетвоення;
- множина містить зворотне перетворення до будь-якого перетворення множини;
- множина містить добуток двох перетворень множини.
Порядок групи - число суттєвих параметрів перетворення. Механіка, що базується на абсолютному часі й групі перетворень евклідового простору, називається класичною (н'ютонівською) механікою.
Вимога ізотропності й однорідності трьохвимірного конфігураційного простору приводить до вимоги інваріантності довжини дуги відносно припустимих перетворень простору:
Час є зовнішнім по відношенню до об'єктом, рівняння механіки є інваріантними відносно перетворень Галілея. Групу Галілея можна об'єднати із перетвореннями руху (закон додавання швидкостей).
Уявімо собі, що точка рухається уздовж прямої лінії на якій встановлена системі відліку Це означає, що на цій прямій розташована шкала із відповідними поділками (тобто квантифікацією) та у кожній точці прямої є синхронізовані між собою годинники. Нехай у момент координата точки дорівнює Цю "подію" можна відзначити на декотрій двохвимірній площині точкою із координатами Площина називається простором подій.
Із плином часу координати точки у просторі подій змінюються, навіть якщо точка не змінює свого положення на прямій - за рахунок зміни часу Внаслідок цього існування точки у просторі та часі позначається декотрою лінією у площині Прямою ця лінія буде лише у випадку, якщо точка рухається по прямій із сталою швидкістю, тоді її положення у буде визначатися рівнянням де є положенням точки у момент Якщо точка є нерухомою на прямій (рухається із нульовою швидкістю), то відповідна пряма у площині є паралельною осі
Нехай уздовж прямої із довільною швидкістю рухається інша система відліку така, що у початковий момент початок координат обох систем співпадають, за Тоді координата точки у системі та відповідна координата у системі будуть пов'язані співвідношенням При цьому час у системі відліку та час у системі один і той самий: для однієї і тієї ж події Перетворення або аналогічно називаються перетвореннями Галілея. Диференціюванням по одержуємо де - швидкість точки у системі а - її швидкість у системі Це - принцип додавання швидкостей у класичный механіці, за яким швидкість точки у старій системі відліку дорівнює її швидкості у новій системі, складеною із "переносною" швидкістю тобто швидкістю руху нової системи відносно старої.
Прискорення точки у системі й у системі є однаковими, з чого можна зробити висновок про те, що однакові сили викликають у обох системах однакові наслідки (які описуються другим законом Н'ютона: пропорційність прискорення силі якою було викликане це прискорення). При цьому говорять, що закони механіки є інваріантними відносно перетворень Галілея і називають це законом відносності Галілея.
Скалярний добуток законів збереження та моменту імпульсу дає відмінний від нуля кубічний закон збереження; перетворення Галілея перетворює інтеграл на нуль. Якщо змінити порядок здійснення операцій і спочатку застосувати перетворення Галілея до законів збереження, а згодом перемножимо їх, то одержимо результат, відмінний від нуля.

Тобто маємо некомутативну діаграму

Відтак логіка законів збереження та логіка принципів Галілея дозволяє вийти за межі гіпотетичного принципу Галілея - одержати закон збереження механіки Н'ютона, який не є інваріантним по відношенню до перетворення Галілея.
Група Лоренца
[ред.]Група Пуанкаре
[ред.]Чисельні алгоритми
[ред.]Алгоритмом є текст, який з точки зору управління може привести до певного однозначного розвитку подій - процесу виконання алгоритму. Біологічно активні речовини, хімічні каталізатори, інстинкти, етична деонтологія тощо - приклади алгоритмів у широкому сенсі.
Синтаксична сторона відомостей характеризує план їх виразу, їхній склад, структуру, складність та організованість. Семантичний аспект характеризує їх змістове наповнення, їх порівнюваність з декотрими еталонними об'єктами та явищами. Прагматична сторона відомостей характеризує їх здатність впливати на процеси управління у системі з точки зору їх цінності, корисності, чи шкідливості. Вибір того чи іншого способу представлення відомостей означає вибір певної мови. Мова програмування - знакова система для планування поведінки машини. Знакова система - сукупність домовлень, які визначають набір знакових ситуацій. Знакова ситуація - первинне поняття семіотики, її елементами є знак та денотат. Знак - це позначення або ім'я, денотат - значення, зміст. Основу будь-якої мови складає абетка - впорядкована сукупність усіх різних знаків мови (генераторів мови).
Алгоритм задає машині точну інструкцію про виконання у певному порядку декотрої системи операцій, які дозволяють вирішити сукупність задач певного класу. Будь-який алгоритм подає процес розв'язування задачі як послідовність відокремлених простих дій. Дії виконуюься почергово, одна за одною, в усталеному порядку. Ця властивість алгоритму називається дискретністю. Алгоритм приводить від початкових даних до шуканого результату через скінченну кількість кроків (дій); при цьому дані варіюються у відомих межах.
Мова є структурою керуючих впливів у складній системі; речення - конкретний фрагмент таких впливів. Співвідношення не відноситься до співвідношення а до чи У моделі "сенс текст" мова представляється відповідністю між двома нескінченними множинами "текстів" та "сенсів". Елементами першої множини є тексти, елементами другої - також тексти, але на штучній семантичній мові, незалежній від натуральної мови, що підлягає конструюванню. Лінгвістика - це теорія перекладу "сенс текст". Переклад складається з проміжних етапів - рівнів представлення речень натуральної мови, серед яких можна виділити фонетичний (орфографічний), фонологічний, синтаксичний й семантичний. Кожний з рівнів, за винятком орфографічного, задається своєю формальною мовою; на кожному з рівнів початкове речення має формальний образ, що називається представленням речення - фонологічним, морфологічним тощо.
При виконанні чисельних розрахунків на комп'ютері зазвичай виникає проблема представлення нескінченної множини дійсних чисел у комп'ютері із скінченною пам'яттю й обмеженою довжиною слова. Найбільш розповсюдженим рішенням цієї проблеми у чисельному аналізі є наближення дійсних чисел за використання скінченної множини чисел із рухомою комою. Множина чисел із рухомою комою характеризується основною лічбою точністю та областю значень експоненти де параметри залежать від комп'ютера. Кожне число з рухомою комою може бути представленим у вигляді де цілі числа задовільняють нерівностям та якщо вимагається, щоб для усіх то будемо мати справу із нормалізованими числами із рухомою комою (включаючи нуль) чисельністю Зрозуміло, що множина не є неперервною та нескінченною множиною. Сума (або добуток) чисел та з множини не може належати множині і повинна бути наближена найближчим числом із рухомою комою. Різниця між істинним й наближеним значенням суми (або добутку) є помилкою округлення. Також потрібно відзначити, що операції додавання й множення у не є асоціативними і закон дистрибутивності не виконується. Таким чином, у чисельному аналізі потрібно ретельно оцінювати помилки округлення (й обчислювати їх границі), які виникають при роботі будь-якого алгоритму, а не зосереджуватися лише на самому алгоритмі та його ефективності.
Чіткі поняття алгортму й ефективної обчислюваності, які є у теоретичній математиці, не пристосовані до потреб обчислювальної (прикладної) математики. Під алгоритмом розуміється точне визначення порядку виконання системи операцій для вирішення відповідного класу задач. Властивості алгоритму:
- дискретність; алгоритм є процесом послідовної побудови об'єктів, який здійснюється за дискретний час таким чином, що у початковий момент задається початковий набір об'єктів, а у кожний наступний момент з набору, який існував у попередній момент, по визначеному закону (програмі) отримується новий набір об'єктів; будь-який алгоритм складається з окремих кроків; кожний крок обов'язково завершується;
- елементарність кроків полягає у тому, що закон отримання наступного набору об'єктів з попереднього повинен бути простим й локальним;
- спрямованість: необхідно вказати, що потрібно вважати результатом виконання алгоритму;
- детермінованість - система скінченного числа вказівок про дії на різних етапах обчислень представляє собою детермінований процес, який може бути відтворений
- масовість - єдиний заданий порядок дій вирішує не одну індивідуальну задачу, а серію (потенційно нескінченну) однотипних задач; початковий набір об'єктів обирається з потенційно нескінченної множини - множини усеможливих початкових даних даного алгоритму; при цьому початковими даними для алгоритму можуть бути лише так звані конструктивні об'єкти (об'єкти, які сконструйовані з декотрих початкових елементарних (синкретичних) об'єктів з фіксованої точно визначеної скінченної множини за фіксованими правилами таким чином, що будова конструктивного об'єкта може бути повністю описана декотрим текстом на відповідній мові);
- уведення та вивід - на вході до алгоритму подаються відомості у відповідному форматі; наприклад, у теоретичній математиці вважається, що на вхід до алгоритму подаються підмножини де - множина цілих додатних чисел; таким чином, множина представляє собою сукупність -векторів із натуральними координатами; вихід алгоритму - результат виконання алгоритму; зазвичай вважається, що в якості вихідних відомостей отримується підмножина Іншими словами, алгоритм приписує спосіб обчислення функції, заданій на множині цілих додатних чисел яка приймає цілі додатні значення. Для однієї і тієї самої функції таких способів може бути багато, і виявляється, що серед них є типовий спосіб: за будь-якого опису алгоритму обчислення функції можна сконструювати поліном із цілими коефіцієнтами такий, що у тому випадку, якщо існують цілі числа із умовою Знаючи та можна віднайти перебиранням векторів по черзі. Можна проаналізувати саму ідею детермінованого процесу обчислень, що приводить до висновку, що цей процес може бути розкладеним у множину елементарних кроків, і функції, обчислювані за допомогою послідовного виконання цих кроків (тобто ітерацій), вичерпують функції, обчислювані будь-яким іншим алгоритмічним способом.
Наприклад, множиною конструктивних об'єктів можна вважати множину слів у скінченній абетці. Елементарними початковими елементами, з яких будуються конструктивні об'єкти, є літери абетки, а спосіб конструювання полягає у побудові скінченних ланцюжків з літер, тобто слів. Зокрема, множина натуральних чисел є прикладом множини конструктивних об'єктів, оскільки натрульні числа можна зображувати словами у однолітерній абетці тобто - слово - слово - слово - слово тощо. Множини цілих й раціональних чисел можуть також розглядатися як множини конструктивних об'єктів.
Існування алгоритмічно невирішуваних задач (наприклад, тотожності слів у групах у загальному випадку) й формально недоказовуваних істин було першим фундаментальним відкриттям теорії обчислюваності (якщо не брати до уваги саму систему основних понять цієї теорії). До багатьох математичних визначень можна додати умову обчислюваності операцій, що входять до них (тобто додати умову конструктивності об'єктів). Нині існують конструктивні варіанти аналізу. Конструктивна математика покликана не замінити класичну, а стати її частиною.
Система комп'ютерної алгебри. Система комп'ютерної алгебри - технологія символьних перетворень математичних формул обчислювальними машинами. Наприклад, вираз за символьних обчислень приводиться до вигляду Символьні спрощення алгебричних виразів є основою комп'ютерної алгебри. Тобто словосполученням "комп'ютерна алгебра" пояснюється здатністю комп'ютерів маніпулювати математичними виразами, заданими символьно, а не чисельно, подібно до того, як це робиться у алгебрі з допомогою ручки і паперу. За Р.Хеммінгом, "мета обчислень у проникненні до суті, а не у цифрах". Таке проникнення до суті досягається іноді за обчислення значень математичних виразів, однак у багатьох випадках при використанні алгебриних засобів співвідношення між величинами стають зрозумілішими.
Символьне диференціювання, що використовує правила обчислення похідної від суми, добутку й частки, також повинне входити до будь-якої системи комп'ютерної алгебри. Вирази типу чи повинні замінятися числом Варто зауважити, що комп'ютерна алгебра дозволяє визначати правила, наприклад, реалізації зовнішнього добутку чи дужки Лі. Система комп'ютерної алгебри повинна, перш за все, працювати із такими типами даних, як довгі цілі числа, раціональні, комплексні числа, кватерніони тощо. До основи символьної частини системи необхідно покласти спрощення виразів, наприклад,
У більшості систем символи є переставними, тобто Наприклад, вираз повинен перетворюватися на вираз
Хоча системи комп'ютерної алгебри існують тривалий час і постійно оновлюються, вони можуть містити деякі характерні помилки й обмеження. Зокрема, за обчислення виразу декотрі системи комп'ютерної алгебри можуть видати результат хоча насправді результат дорівнює Якщо запропонувати системі обчислити невизначений інтеграл де за цей інтеграл отримається за формулою а за отримаємо Ще одна невизначеність може виникнути за обчислення Якщо розглядати за і згодом, застосовуючи правило Лопіталя, знаходимо в якості можливого визначення Також деякі системи, обчислюючи вираз за можуть давати невірний результат (правильний дорівнює ). При вирішенні рівняння система повинна розрізняти випадки й
Як вже зазначалося, для ятого, щоб представляти цілі числа довільної точності й виконувати точні арифметичні операції, необхідно увести відповідні структури даних (чи користуватися модулярною арифметикою).











































































































































































![{\displaystyle [L,U],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/793345412904b7e58bbbbc30641139226156de00)

































![{\displaystyle x-2\cdot x+{\frac {d}{dx}}[(x-a)^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcb80200ac16b9e70296426a241152423c5eb50a)


























