Розв'язник вправ по дискретній математиці/Графи/Хроматичне число

Ця версія книжки "Розв'язник вправ по дискретній математиці" призначена для друку
Ви не побачите це повідомлення при попередньому перегляді цієї сторінки.

Розв'язник вправ по дискретній математиці. Графи. Хроматичне число

Хроматичне число графа G — мінімальна кількість кольорів, в які можна розфарбувати вершини графа G таким чином, щоб кінці будь-якого ребра мали різні кольори. Позначається як χ(G).

Приклади на хроматичне число

Обчисліть хроматичне число для графу:

N₁ (складається з однієї вершини).

Розвязок.
Граф N - це граф без ребер. Тому для графу, що складається тільки з однієї вершини, хроматичне число 1.
Відповідь - 1.

N_k (складається з k незв'язних вершини).

Розвязок.
Ми маємо граф, який складається тільки з k-вершин без ребер. Тому, хроматичним числом для графа N_k - є 1.
Відповідь - 1.

K₂ (дві вершини з'єднані ребром).

Розвязок.
Уявимо, що маємо граф G у вигляді відрізку. Тому, розфарбовуємо вершини у 2 кольори. І маємо, що це і є мінімальною кількістю кольорів, в які можна розфарбувати вершини графа G таким чином, щоб кінці будь-якого ребра мали різні кольори.

Відповідь - 2.

K₃ (повний граф).

Розвязок.
Граф K₃ - це трикутник.
Припустимо, що вершину А ми розфарбували у червоний колір, з неї виходить ще 2 ребра, які потім з'єднанні ще 1 ребром, тому, щоб кінцівки цих ребер були різних кольорів, розфарбуємо іх у зелений та синій кольори. Таким чином, для графу K₃ хроматичним числом - є 3.
Відповідь - 3.

W₄ (колесо).

Розвязок.
Граф W₄ - це трикутник з вершиною в центрі. Таким чином, якщо починати розфарбовувати саме з центральної вершини, виходить, що вона з'єднана з усіма іншими. Тому хроматичним числом для графу W₄ - є 4.
Відповідь - 4.

S₄ (зірка).

Розвязок.
Граф S₄ - це граф W₄, але без ободка. Тому, розмірковуючи аналогічно до W₄, спочатку розфарбуємо центр у чевроний, а потім усі інші вершини у синій, бо вони не з'єднані між собою. Таким чином, хроматичним числом для графу S₄ - є 2.
Відповідь - 2.

C₄ (цикл).

Розвязок.
Граф C₄ - це квадрат. Тому, задля знаходження хроматичного числа для цього графу, розфарбуємо 2 вершини, які з'єднані умовною діагоналлю у синій колір, а інші у червоний.
Відповідь - 2.

Хроматичний поліном

Хроматичний многочлен з'являється, якщо розглядати кількість відмінних розфарбувань позначеного графа як функцію від кількості доступних кольорів t. Виявилось, що ця функція завжди буде поліномом від t.

Хроматичний поліном

Приклади на хроматичний поліном

Обчисліть хроматичний многочлен для графу:

N₁ (складається з однієї вершини).

Розвязок.
Граф N₁ - це 1 вершина без ребер. Тому, поліномом для цього графу - є t.
Відповідь - t.

N_k (складається з k незв'язних вершини).

Розвязок.
Граф N₁ - це k-вершина без ребер. Тому, поліномом для цього графу - є t.
Відповідь - t.

K₂ (дві вершини з'єднані ребром).

Розвязок.
Граф K₂ - це відрізок. Тоді одну кінцівку можна розфарбувати у t кольорів, а іншу вже у t-1. Таким чином, многочленом для K₂ - t*(t-1).
Відповідь - t*(t-1).

K₃ (повний граф).

Розвязок.
Розмірковуючи аналогічно, як для K₂, получаємо поліном t*(t-1)*(t-2).
Відповідь - t*(t-1)*(t-2).

W₄ (колесо).

Розвязок.
Розглянемо граф W₄. Центральну вершину ми можемо розфарбувати у t-кольорів, а інші у (t-1), (t-2) i (t-3), бо вони з'єднанні між собою. Таким чином, многочлен для графу W₄ - t*(t-1)*(t-2)*(t-3).
Відповідь - t*(t-1)*(t-2)*(t-3).

S₄ (зірка).

Розвязок.
Якщо розфарбовувати граф S₄ з центру, то цю вершину ми можемо побачити в t кольорах, а інші у (t-1). Таким чином, поліном для S₄ - t*(t-1)^3.
Відповідь - t*(t-1)^3.

L₄ (ломана).

Розвязок.
Припустимо, що маємо декілька з'єднаних між собою відрізків. Таким чином, якщо поліном від K₂ - t*(t-1), то L₄ - це 2 з'єднаних відрізка і поліном виглядає так: t^2*(t-1)^2.
Відповідь - t^2*(t-1)^2.

C₄ (цикл).

Розвязок.
Граф C₄ = L₄ - K_3.
C₄ = t^2*(t-1)^2 - t*(t-1)*(t-2) = t*(t^3-3*t^2+2*t - 2)
Відповідь - t*(t^3-3*t^2+2*t - 2).

K_n (цикл).

Розвязок.
Якщо провести аналогію з K₂, та K₃, то маємо, що K_n має поліном вигляду: t*(t-1)*(t-2)*...*(t-(n-1))
Відповідь - t*(t-1)*(t-2)*...*(t-(n-1)).

Рекурентні формули для хроматичного поліному

Приклад. Знайти хроматичний поліном графа, показаного на мал. 12.8.

Рішення. Якщо граф майже повний, то, додавши декілька ребер, одержимо хроматичний поліном у вигляді суми факторіальних ступенів. Якщо ж ребер мало, то для отримання порожнього графа потрібно видалити тільки декілька ребер. Такі дії називаються хроматичною редукцією.

мал. 12.9

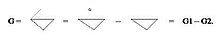
1. Хроматична редукція по порожніх|пустих| графах. Видаляючи ребра і ототожнюючи відповідні вершини (стягуючи ребра), зведемо початковий граф до порожного графу. Спочатку розкладемо граф на два, прибравши, а потім стягнемо ребро 1-3. Тепер ми маємо (мал.12.9) : трикутник з точкою - трикутник. Так, як точка з трикутником є незв'язним графом, то ми маємо: t*(t*(t-1)*(t-2)) - (t*(t-1)*(t-2).

Відповідь - t*(t*(t-1)*(t-2)) - (t*(t-1)*(t-2).

Розкладання (12.9) називається хроматичною редукцією графа по порожніх графах.

2. Хроматична редукція по повних|цілковитих| графах. Додавши до зображеного на мал. 12.8 графа ребро 1–4, одержимо граф із великим числом ребер. Потім в початковому графі ототожнимо вершини 1 і 4. В результаті отримаємо двa графa. (мал 12.10)

мал. 12.10

Ототожнення вершин приводить до зменшення порядку і інколи розміру графа. Другий граф – це повний граф, його перетворювати більше не потрібно. До першого графа додамо ребро 1–2 і ототожнимо вершини 1 і 2: мал. 12.11

мал. 12.11

Хроматичний поліном прийме вигляд: K₄+2K₃ = t*(t-1)*(t-2)*(t-3) + 2*t*(t-1)*(t-2)

Відповідь - t*(t-1)*(t-2)*(t-3) + 2*t*(t-1)*(t-2).

Обчислення хроматичного поліному для циклу, колеса і дерева

хроматичний многочлен для C_n (цикл).

Розвязок.
Нехай C_n - цикл довжини n. Тоді хроматичний многочлен циклу P(C_n,x)=(x−1)ⁿ+(−1)ⁿ(x−1)
Доведемо по індукції за кількістю вершин. База індукції: розглянемо випадок n = 3:
P(C₃,x)=x(x−1)(x−2)=(x³−3x²+3x−1)−(x−1)=(x−1)³+(−1)³(x−1), що задовольняє формулюванні теореми. Індукційний перехід: нехай P(C_k,x)=(x−1)^k+(−1)^k(x−1). Розглянемо випадок n=k+1.
По теоремі про рекуррентну формулу для хроматичних многочленів: P(C_k+1,x)=P(Ck_+1∖e,x)−P(C_k+1/e,x) (де e - будь ребро C_k+1/e). Зауважимо, що граф C_k+1/e ізоморфний C_k, а граф C_k+1∖e є простим ланцюгом. Тоді P(C(_k+1,x)=P(T_k+1,x)−P(C_k,x)=x(x−1)^k−(x−1)^k−(−1)^k(x−1) = (x−1)^k+1+(−1)^k+1(x−1).
Відповідь: (x−1)^k+1+(−1)^k+1(x−1).

хроматичний многочлен для W_n (колесо).

Розвязок.
Нехай W_n — колесо с nл, вершинами. Вибравши і зафіксувавши один з x кольорів на вершині, пов'язаної з усіма іншими, маємо P(C_n−1,x−1) варіантів розмальовки графа. Тоді хроматичний многочлен колеса P_Wn(x)=x⋅PC_n−1(x−1)=x((x−2)⁽ⁿ⁻¹⁾−(−1)ⁿ(x−2)).
Відповідь: x((x−2)⁽ⁿ⁻¹⁾−(−1)ⁿ(x−2)).

хроматичний многочлен для дерева.

Граф з n вершинами є деревом тоді, коли P(G,x)=x(x−1)ⁿ⁻¹

Розвязок.
Доведення:
⇒
Спочатку покажемо, що хроматичний многочлен будь-якого дерева T з n вершинами є x (x-1) n-1. Доказ за індукцією по числу n. Для n = 1 і n = 2 результат очевидний. Припустимо, що P (T ', x) = x (x-1)^n-2 для будь-якого дерева T' з кількістю вершин рівним n-1. Нехай uv - ребро дерева T, таке що v є висячої вершиною. Хроматичний многочлен дерева T без ребра uv дорівнює P (T / uv, x) = x (x-1)^n-2 за нашим припущенням. Вершину v можна розфарбувати x-1 способом, так як її колір повинен тільки відрізнятися від кольору вершини u. Разом: P (T, x) = (x-1) P (T / uv, x) = x (x-1)^n-1.
⇐ Назад, нехай G - граф, у якого P (G, x) = x (x-1) n-1. Тоді вірні два наступних твердження

Граф G зв'язний, тому що якщо було б дві компоненти зв'язності (або більше), то P (G, x) ділився б на 2 без залишку. У графі G кількість ребер одно n-1, так як по одній з теорем про коефіцієнти хроматичного многочлена, кількість ребер в графі відповідає коефіцієнту при x^n-1, взятому зі знаком мінус. У нашому випадку, цей коефіцієнт зручно шукати, використовуючи біном Ньютона: P(G,x)=x(x−1)ⁿ⁻¹=x(xⁿ⁻¹−(n−1,1)xⁿ⁻²+(n−1,2)xⁿ⁻³−...+(−1)ⁿ⁻¹)=xⁿ−(n−1)xⁿ⁻¹+...+(−1)ⁿ⁻¹x Из этих двух утверждений (связность и n-1 ребро) следует, что граф є деревом.

Коефіціенти хроматичного поліному

Теорема 1. Коефіцієнти хроматичногоЗ цих двох тверджень (зв'язність і n-1 ребро) слід, що граф є деревом. полінома складають знакозмінну послідовність.

Теорема 2. Абсолютна величина другого коефіцієнта хроматичного полінома рівна числу ребер графа.

Теорема 3. Найменше число i, для якого відмінний від нуля коефіцієнт при в хроматичному поліномі графа G, рівне числу компонент зв'язності графа G.