Основні числові системи/Натуральні числа

Логотип Вікіпедії

Вікіпедія має пов'язану з цією темою інформацію на сторінці Натуральні числа

Натуральні числа $\mathbb {N}$ застосовуються для двох головних цілей: для лічби та для впорядкування. Множина натуральних чисел вважається нескінченною: $\mathbb {N} =\{1,2,3,4,5,...,\infty \}.$ Потужність множини натуральних чисел позначають символом $\aleph _{0}.$

Вступ

Перераховуючи елементи даної скінченної множини $A$, ми ставимо цій множині у відповідність деяке натуральне число, $A\to \mathbb {N} ,$ і таким чином відповідаємо на запитання про те, скільки елементів міститься у цій множині. Впорядковуючи множину за допомогою натуральних чисел, занумеровуюмо її елементи як перший, другий, третій тощо. Таким чином, довільна множина $A$ називається зліченною, якщо її елементи можна занумерувати натуральними числами, тобто $a_{\mathbb {N} }=a_{1},a_{2},a_{3},...\,.$ Множина натуральних чисел $1,\,2,\,3,...,n,\,n+1,...$ розглядається як множина елементів (які утворюються з символів абетки $\{0,1,2,3,4,5,6,7,8,9\},$ тобто цифр), на якій визначене відношення безпосереднього слідування: натуральне число $b$ безпосередньо слідує за натуральним чином $a$ ($2$ слідує безпосередньо за 1, 3 слідує безпосередньо за 2 тощо).

Множина натуральних чисел має наступні властивості:
1. існує натуральне число $1$ (одиниця), яке не слідує за жодним іншим натуральним числом, тобто число $1$ є мінімальним елементом множини $\mathbb {N} .$
2. Для будь-якого натурального числа $n$ існує лише одне натуральне число $n+1$, що безпосередньо слідує за ним.
3. Будь-яке натуральне число слідує не більш ніж за одним натуральним числом.
4. Кожна множина натуральних чисел $M$, яка містить число $1$ і яка з кожним числом $n,$ що міститься у ній, містить також і слідуюче за цим числом число $n+1,$ співпадає із множиною усіх натуральних чисел, тобто $M=\mathbb {N}$.

Ці чотири властивості називаються аксіомами Пеано. Яким є їхній зміст? У першій аксіомі стверджується, що у множині натуральних чисел є число, яке не слідує за жодним іншим числом цієї множини. Друга аксіома встановлює нескінченність множини натуральних чисел. Щоправда, для цього необхідно ще показати, що $n+1\neq n.$ У третій аксіомі мова йде про те, що жодне натуральне число не може слідувати за двома різними числами. Четверта аксіома називається аксіомою математичної індукції. Вона лежить в основі методу індуктивного доказу математичних тверджень, який називається методом математичної індукції.

Як говорилося у другій аксіомі, $n+1\neq n.$ Запевнимося у цьому й розгляньмо $M$ - множину усіх тих натуральних чисел $n,$ для кожного з яких $n+1\neq n.$ Тоді $1\in M,$ оскільки за першою аксіомою $1+1\neq 1.$ Справді, $n+1+1\neq n+1,$ оскільки у протилежному випадку, за третьою аксіомою, мала б місце рівність $n+1=n$ та, відповідно, $n$ не належало би до $M.$ Таким чином, можина $M$ задовільняє умовам аксіоми індукції і тому $M=\mathbb {N} ,$ а відповідно для будь-якого $n$ справедлива нерівність $n+1\neq n.$

Якщо множина є рівночисельною підмножині множини $B,$ то говорять, що кардинальне число $A$ не більше кардинального числа $B.$ Нехай $A$ та $B$ - такі множини, що чисельність $A$ дорівнює чисельності підмножини множини $B,$ а чисельність $B$ дорівнює чисельності підмножини множини $A.$ У такому випадку кажуть, що $A$ та $B$ рівночисельні (рівнопотужні, тобто їхні кардинальні числа є рівними). Множина називається зліченною, якщо між нею та множиною натуральних чисел можно встановити взаємно однозначну відповідність. Зрозуміло, що якщо $\mathbb {N}$ - нескінченна множина, то й $2\cdot \mathbb {N}$ - також нескінченна множина. Між цими множинами можна встановити взаємно однозначну відповідність: ${\begin{matrix}n\\2\cdot n\end{matrix}}{\begin{pmatrix}1&2&3&4&5&...&\infty \\2&4&6&8&10&...&\infty \end{pmatrix}},$ для $n\in \mathbb {N} .$ Таким самим чином множина непарних натуральних чисел є зліченною: ${\begin{matrix}2\cdot n\\2\cdot n-1\end{matrix}}{\begin{pmatrix}2&4&6&8&10&...&\infty \\1&3&5&7&9&...&\infty \end{pmatrix}}$ для $n\in \mathbb {N} .$

Рівночисельність є рівносильним відношенню еквівалентності. Відношення рівночисельності розбиває усі множини на класи еквівалентності, занумеровані кардинальними числами (коротше, кардиналами). Інакше кажучи, кардинальне число (кардинал) множини $X$ - це клас еквівалентності (шар) множин, рівночисельних $X.$ Тобто рівночисельні множини входять до одного й того ж шару. Кожний шар - визначається окремим кардинальним числом. Зрозуміло, що таке під таким розшаруванням йдеться про порядок: $X_{\mathrm {card} (X)}\subset X_{\mathrm {card} (X)+1}\subset X_{\mathrm {card} (X)+2}\subset ...$ При цьому вважається, що $X$ - надзвичайно чисельна множина, чисельність якої може бути за необхідності збільшена настільки, наскільки потрібно. У такому випадку $X$ називають універсумом. Нажаль, існування універсуму рівносильно існуванню сильно недосяжних кардиналів у теорії множин. З аксіоматичної ж точки зору "клас еквівалентності множин, рівночисельних множині $X$" не є множиною. Тим не менш, "множину кардиналів, менших даного" визначити можна.

Дії над натуральними числами

Додавання натуральних чисел

Бінарна операція на множині $A$ - це декотре відображення $f:A\times A\to A.$ Зокрема, операція додавання натуральних чисел - це декотре відображення $f:\mathbb {N} \times \mathbb {N} \to \mathbb {N} .$ Тому визначення додавання на множині $\mathbb {N}$ полягає у відшуканні відображення $f:\mathbb {N} \times \mathbb {N} \to \mathbb {N} ,$ наділеного відомими властивостями додавання натуральних чисел. Таким чином, при додаванні розглядається добуток $\mathbb {N} \times \mathbb {N} ,$ що складається з впорядкованих пар натуральних чисел $(a,b),$ і множина натуральних чисел $\mathbb {N} .$ Число, у яке відображається пара $(a,b)$ за відображення $f:\mathbb {N} \times \mathbb {N} \to \mathbb {N} ,$ позначають виразом $a+b$ і називають сумою доданків $a$ та $b.$

За будь-яких значень доданків $a$ та $b$ сума не змінюється, якщо ці доданки поміняти місцями: $a+b=b+a.$ Ця властивість додавання називається переставною і формулюється наступним чином: від перестановки доданків сума не змінюється. На відміну від додавання, для віднімання натуральних чисел переставна властивість не є властивою: $a-b\neq b-a.$

Якщо до суми доданків $a$ та $b$ додати третє число, то отримаємо число, яке дорівнює сумі першого числа і результату додавання другого та третього чисел: $(a+b)+c=a+(b+c).$ Із сказаного можна зробити висновок, що доданки можна переставляти місцями і об'єднувати у будь-яку групу (групувати). З цього також можна зробити наступний висновок: сума двох натуральних чисел є завжди більшою від кожного з доданків, тобто $a+b>a$ та $a+b>b.$ У загальному випадку $a+b\neq b$ та $a+b\neq a.$

Множення натуральних чисел

Бінарна операція множення на множині натуральних чисел є відображенням $f:\mathbb {N} \times \mathbb {N} \to \mathbb {N} ,$ яке кожній парі натуральних чисел $(a,b)$ ставить у відповідність натуральне число, яке позначається виразом $a\cdot b$ і називається добутком множників $a$ та $b.$

Множення натуральних чисел підпорядковується переставному законові: $a\cdot b=b\cdot a.$ Тобто добуток не змінюється від перестановки множників. Щоб помножити добуток $(a\cdot b)$ на третє число $c,$ достатньо перше число $a$ помножити на добуток $(b\cdot c).$ Тобто множення підпорядковується сполучному законові: $(a\cdot b)\cdot c=a\cdot (b\cdot c)=(a\cdot c)\cdot b.$ Сполучна і переставна властивості множення дають змогу групувати множники: $7\cdot 2\cdot 10=2\cdot 7\cdot 10=10\cdot 2\cdot 7=20\cdot 7=140.$

Щоб помножити суму $(a+b)$ (або різницю $(a-b)$) на число $c,$ необхідно кожний доданок (зменшуване та від'ємник відповідно) помножити на це число і отримані добутки додати (відняти). Тобто

$(a+b)\cdot c=a\cdot c+b\cdot c,\quad \quad (a-b)\cdot c=a\cdot c-b\cdot c.$

Ця властивість множення називається розподільною властивістю множення. Від перестановки множників добуток не змінюється: $(a+b)\cdot c=c\cdot (a+b).$

Ділення натуральних чисел також підпорядковується розподільному законові: щоб поділити суму (різницю) натуральних чисел на натуральне число, необхідно кожний доданок (зменшуване і відємник відповідно) поділити (якщо це можливо) на це число і знайдені частки додати (відняти). Тобто

$(a+b):c=a:c+b:c,\quad \quad (a-b):c=a:c-b:c.$

Найменше спільне кратне (НСК)

Розкладання числа на множники - представлення його у вигляді добутку множників. Зокрема, ми можемо вимагати, щоб усі множники при розкладі даного числа були простими числами. Розгляньмо числа $204,\,24,\,27,\,256.$ Розкладімо їх на додатні прості множники, послідовно ділячи їх (та отримані від ділення частки) на найменші невід'ємні прості числа. Це зручно робити наступним чином: провести вертикальну лінію і ліворуч послідовно (згори вниз) записати число та отримані частки від ділення на прості числа, а праворуч - прості числа навпроти відповідних дільників. Таким чином, праворуч ми отримаємо прості дільники (прості множники). У прикладі із числом $24$ ми спочатку ділимо його на найменший простий дільник - на просте число $2.$ Отриману частку, тобто число $12,$ ми далі ділимо на найменше просте число тощо.

Найменше спільне кратне двох натуральних чисел $a$ та $b$ - найменше натуральне число, яке ділиться націло на кожний з двох даних натуральних дільників. Нехай $a=3,$ a $b=6.$ Найменшим натуральним числом, яке ділиться націло на $3$ та на $6,$ є число $6.$ Пишуть НСК(3;6)=6. Для чисел $a=8$ та $b=15$ НСК(8;15)=120. НСК зручно знаходити за наступним правилом:

• розкласти дані числа на прості множники;
• виділити степені, основи яких є присутніми лише у одному з розкладів на прості множники;
• помножити виділені степені між собою.

Розгляньмо числа $18,\,24,\,30.$ Розкладімо їх на прості множники:

• $18=2^{1}\cdot 3^{2};$
• $24=2^{3}\cdot 3^{1};$
• $30=2^{1}\cdot 3^{1}\cdot 5^{1}.$

Далі, виділимо степені основ, які присутні лише у одному з розкладів: тобто $3^{2},\,2^{3},\,5^{1}.$ Перемножуючи їх, отримуємо НСК(18; 24; 30)$=2^{3}\cdot 3^{2}\cdot 5=360.$

Якщо $a$ та $b$ - прості числа, то НСК(a; b) буде їх добуток, $a\cdot b.$ Якщо число $a$ є дільником числа $b$ (тобто якщо число $b$) ділиться на число $a$ націло, то НСК(a; b)$=b.$

Розгляньмо декілька прикладів:

• НСК(25; 32; 7);
  • розклад на прості множники: $25=5^{2},\,32=2^{5},\,7=7^{1}\cdot 1;$
    • добуток степенів основ, присутніх лише у одному із розкладів, НСК(25, 32, 7)$=5^{2}\cdot 2^{5}\cdot 7=5600.$
• НСК (8; 9; 15);
  • розклад на прості множники: $8=2^{3},\,9=3^{2},\,15=3^{1}\cdot 5^{1};$
    • НСК(8; 9; 15)$=3^{2}\cdot 3^{1}\cdot 5^{1}=135.$
• НСК (7; 13);
  • числа $7$ та $13$ є простими, тому НСК(7; 13)$=7\cdot 13;$
• НСК (54; 6);
  • число $54$ ділиться на $6$ і тому НСК(54; 6)=$54.$

Найбільший спільний дільник (НСД)

Найбільше натуральне число, на яке діляться дані натуральні числа, називається найбільшим спільним дільником для цих чисел. Наприклад, для чисел $10,\,15,\,230$ найбільшим спільним дільником буде число $5.$ Тобто НСД(10; 15; 230)$=5.$ Взагалі, щоб віднайти НСД даних чисел, зручно користуватися наступним правилом:

• розкласти ці числа на прості дільники: $10=2^{1}\cdot 5^{1},\,\,10=5^{1}\cdot 3^{1},\,\,230=2^{1}\cdot 5^{1}\cdot 23^{1}$;
• виділити степені, основи яких є спільними простими дільниками даних чисел: у нашому випадку лише число $5^{1}$ є спільним простим дільником чисел $10,\,15$ та $230$;
• виділити з розкладу найменші показники степенів однакових основ;
• перемножити їх.

Розгляньмо декілька прикладів:

• НСД(12; 32; 44);
  • розкладемо числа на прості множники: $12=2^{2}\cdot 3^{1},\,\,32=2^{5},\,\,44=2^{2}\cdot 11^{1};$
    • степінь $2$ із основою $2$ (тобто $2^{2}=4$) є НСД(12; 32; 44);
• НСД(455; 770); розкладімо дані числа на прості множники: $455=5^{1}\cdot 7^{1}\cdot 13^{1},\,\,770=2^{1}\cdot 5^{1}\cdot 7^{1}\cdot 11^{1};$
  • лише числа $5^{1}$ та $7^{1}$ є простими множиками чисел $455$ та $770,$ тому НСД(455; 770)$=7\cdot 5=35.$
• НСД (17; 19; 43);
  • числа $17,\,19,\,43$ є взаємно простими, оскільки найбільшим спільним дільником для них є число $1.$

Округлення натуральних чисел

Нехай чисельність населення міста, встановлена в результаті перепису населення, становить $461\,441$ чоловік. Це число незабаром може стани іншим, наприклад, в результаті епідемії деякої хвороби. У ньому зміняться цифри одиниць, десятків, а згодом й сотень. Відтак на запитання, скільки людей проживає у даному місті, відповідають: близько $461\,000.$ Це число називається наближенням значення числа $461\,441$ і записується за допомогою символа $\approx ,$ тобто $461\,441\approx 461\,000.$ Заміна числа його наближеним значенням називається округленням, а результат округлення - округленим числом до деякого розряду, скажімо, $231\,2\color {red}{1}\color {black}{3\,742}$ коли усі цифри праворуч від обраного розряду (до якого мається намір округлювати дане число) замінюються нулями, тобто $321\,21\color {blue}{0\,000}.$ Наприклад, швидкість світла у вакуумі становить $299\,792\,458$ метрів на секунду. Цю величину замінюють її наближеним значенням - $\approx 300\,000\,000$ м/с або $300\,000$ км/с.

При округленні користуються наступним правилом: якщо перша ліворуч з цифр, що замінюються нулями, менша за $5$, то остання залишена цифра не замінюється. Нехай число $21\,394$ необхідно округлити до десятків, тобто $21\,3\color {red}{8}\color {black}{4}.$ У цьому випадку $4<5,$ тому $\approx 21\,3\color {green}{8}\color {blue}{0}.$ Якщо ж маємо число $21\,385$ і нам потрібно округлити його до десятків, тобто $21\,3\color {red}{8}\color {black}{5},$ то у цьому випадку розряд десятків збільшиться на одиницю, $\approx 21\,3\color {green}{9}\color {blue}{0}.$ Зрозуміло, що якщо число, яке позначає сусідня цифра праворуч від обраного розряду, більше $4,$ то обраний розряд збільшується на одиницю; якщо менше $5$ (тобто дорівнює $4$ або менше), то обраний розряд залишається незмінним.

Розширена множина натуральних чисел

Розширеною множиною натуральних чисел називається множина натуральних чисел, що містить число $0,$ тобто $\mathbb {N} \cup \{0\}.$ Те, що число $0$ у загальному випадку не належить до множини натуральних чисел пов'язане із тим, що множина натуральних чисел слугує для лічби, підрахунку предметів, а число $0$ позначає відсутність предметів взагалі. При цьому не потрібно плутати число $0$ та цифру $0,$ яка позначає відсутність відповідного розряду при записі числа. За уведення числа $0$ впроваджують правило, згідно з яким забороняється здійснювати ділення чисел на чило $0.$ Причина такої заборони стане зрозумілою згодом. Добуток від множення довільного числа $a$ на число $0$ дорівнює нулю, тобто $a\cdot 0=0.$ Віднімання чи додавання до числа $a$ нуля дорівнює самому цьому числу $a,$ тобто $a+0=a$ та $a-0=a.$

Факторіал - добуток усіх натуральних чисел від $1$ до даного натурального числа $n.$ Символічно факторіал позначається за допомогою знаку оклику, $n!=1\cdot 2\cdot 3\cdot \cdot \cdot n-1\cdot n=\prod _{i=1}^{n}i.$ Наприклад, $5!=5\cdot 4\cdot 3\cdot 2\cdot 1=120$ (читається "П'ять факторіал дорівнює сто двадцять"). Вважають, що $0!=1.$

Факторіал $m!$ дорівнює числу перестановок елементів множини $A$ із кардинальним числом $\mathrm {card} (A)=m.$ Наприклад, нехай $A=\{\spadesuit ,\clubsuit ,\heartsuit ,\diamondsuit \}.$ Зрозуміло, що чисельність $A$ дорівнює $4.$ Розгляньмо число способів перестановки елементів множини $A:$

$\{\spadesuit ,\clubsuit ,\heartsuit ,\diamondsuit \},\quad \{\diamondsuit ,\spadesuit ,\clubsuit ,\heartsuit \},\quad \{\heartsuit ,\diamondsuit ,\spadesuit ,\clubsuit \},\quad \{\clubsuit ,\heartsuit ,\diamondsuit ,\spadesuit \},$

$\{\spadesuit ,\diamondsuit ,\clubsuit ,\heartsuit \},\quad \{\heartsuit ,\spadesuit ,\diamondsuit ,\clubsuit \},\quad \{\clubsuit ,\heartsuit ,\spadesuit ,\diamondsuit \},\quad \{\diamondsuit ,\clubsuit ,\heartsuit ,\spadesuit \},$

$\{\spadesuit ,\heartsuit ,\clubsuit ,\diamondsuit \},\quad \{\diamondsuit ,\spadesuit ,\heartsuit ,\clubsuit \},\quad \{\clubsuit ,\diamondsuit ,\spadesuit ,\heartsuit \},\quad \{\heartsuit ,\clubsuit ,\diamondsuit ,\spadesuit \},$

$\{\spadesuit ,\diamondsuit ,\heartsuit ,\clubsuit \},\quad \{\clubsuit ,\spadesuit ,\diamondsuit ,\heartsuit \},\quad \{\heartsuit ,\clubsuit ,\spadesuit ,\diamondsuit \},\quad \{\diamondsuit ,\heartsuit ,\clubsuit ,\spadesuit \},$

$\{\spadesuit ,\heartsuit ,\diamondsuit ,\clubsuit \},\quad \{\clubsuit ,\spadesuit ,\heartsuit ,\diamondsuit \},\quad \{\diamondsuit ,\clubsuit ,\spadesuit ,\heartsuit \},\quad \{\heartsuit ,\diamondsuit ,\clubsuit ,\spadesuit \},$

$\{\clubsuit ,\heartsuit ,\diamondsuit ,\spadesuit \},\quad \{\spadesuit ,\clubsuit ,\diamondsuit ,\heartsuit \},\quad \{\heartsuit ,\spadesuit ,\clubsuit ,\diamondsuit \},\quad \{\diamondsuit ,\heartsuit ,\spadesuit ,\clubsuit \}.$

Число способів перестановки дорівнює $4!=1\cdot 2\cdot 3\cdot 4=24.$

Перестановка $n$ чисел $1,2,...,n$ (чи $n$ довільних змінних $a_{1},a_{2},...,a_{n}$) називається розташуванням (розміщенням) цих чисел (символів) у певному пордку. Оскільки дані $n$ символів можна занумерувати натуральними числами, то вивчення перестановок будь-яких $n$ чисел можна звести до вивчення перестановок натуральних чисел. Число усіх перестановок з $n$ чисел дорівнює $n!=1\cdot 2\cdot 3\cdot \cdot \cdot n.$

Два числа у перестановці утворюють інверсію, якщо більше число стоїть спереду меншого, якщо ж більше число стоїть спереду меншого, то числа утворюють порядок. Число інверсій визначається наступним чином:

• спочатку читають числа перестановки у порядку їх запису (зліва праворуч);
• для кожного числа рахують, оскільки чисел менших за дане стоїть правіше нього;
• одержані числа додаються.

Наприклад, у перестановці $637412$ число інверсій дорівнює $1+2+1=4.$

Перестановка називається парною чи непарною, в залежності від того, чи буде число інверсій у ній парним чи непарним.

Транспоризцією називається зміна місцями двох чисел перестановки. Транспозиція чисел $i$ та $j$ позначається $(i,j).$ Від будь-якої перестановки $n$ чисел до будь-якої іншої перестановки можна перейти шляхом ряду транспозицій, прочому можна обійтися не більш ніж $n-1$ транспозиціями. Наприклад, від перестановки $53421$ до перестановки $42513$ можна перейти шляхом чотирьох транспозицій: $(5,4),\,(3,2),\,(4,5),\,(2,1),\,(1,3).$

Підстановкою $n$ чисел $1,2,...,n$ (тобто підстановкою степені $n$) називається взаємно однозначне відображення сукупності цих чисел на себе, тобто відображення, за якого кожному числу від $1$ до $n$ відповідає яке-небудь з самих цих чисел, при цьому двом різним числам завжди відповідають два різні числа. Підстановка записується у вигляді таблиці, наприклад, ${\begin{pmatrix}1&3&2&4\\2&3&1&4\end{pmatrix}}.$ У наведеній підстановці $1\to 2,\,3\to 3,\,2\to 1,\,4\to 4.$

В залежності від розташування чисел у верхньому рядку одну і ту саму підстановку можна зписувати багатьма способами, зокрема, підстановки

${\begin{pmatrix}1&2&3\\2&3&1\end{pmatrix}},\quad \quad {\begin{pmatrix}2&3&1\\3&1&2\end{pmatrix}},\quad \quad {\begin{pmatrix}3&2&1\\1&3&2\end{pmatrix}}$

є однією і тою самою підстановкою, де $(1\to 2),\,(2\to 3),\,(3\to 1).$ Кожна підстановка $n$ чисел може бути записана посередництвом $n!$ різних варіантів її запису.

Підстановка є парною, якщо загальне число інверсій у обох рядках є парним, та непарною, якщо число інверсій непарне. Наприклад, підстановка ${\begin{pmatrix}2&3&4&1\\3&1&4&2\end{pmatrix}}={\begin{pmatrix}1&2&3&4\\2&3&1&4\end{pmatrix}}$ у першому записі містить шість інверсій (верхній рядок $1+1+1=3,$ нижній рядок $2+1=3,$ відтак $3+3=6$), а другому записі - дві (у верхньому рядку немає інверсій, у нижньому $1+1=2$). Відповідно, підстановка парна.

Парність визначається наступним чином. Циклом називається послідовність декількох чисел, у якій число при даній підстановці переходить у друге, друге у третє тощо, а останнє число - у перше. Цикл позначається виразом його чисел у дужках. Якщо число переходить саме у себе, то воно утворює цикл. Цикли, які не мають спільних чисел, називаються незалежними. Будь-яку підстановку можна розкласти на незалежні цикли. Наприклад, ${\begin{pmatrix}1&2&3&4\\4&3&2&1\end{pmatrix}}=(14)\,\,(23),$ оскільки $(1\to 4)$ й $(4\to 1)$ та $(2\to 3)$ й $(3\to 2).$

Декрементом $d$ називається різниця між числом $n$ усіх елементів та числом $k$ циклів за її розкладу на цикли: $d=n-k.$ Парність підстановки співпадає із парністю її декремента. У нашому прикладі число елементів $n=4,$ кількість циклів $k-2,$ відповідно, $d=4-2=2.$ Таким чином, підстановка є парною. Число парних підстановок з $n$ елементів дорівнює числу непарних, тобто ${\frac {1}{n}}n!$ (за $n\geq 2$).

Найменше число транспозицій, яке є необхідним для переходу від однієї перестановки $n$ чисел $a_{1},a_{2},...,a_{n}$ до іншої перестановки тих самих чисел $b_{1},b_{2},...,b_{n}$ дорівнює декременту підстановки ${\begin{pmatrix}a_{1}&a_{2}&...&a_{n}\\b_{1}&b_{2}&...&b_{n}\end{pmatrix}}.$ Таким чином, для будь-якох перестановки $n$ чисел існують перестановки тих самих чисел, які не можна перевести у дану перестановку менш ніж $n-1$ транспозиціями.

Порівняння натуральних чисел

Променем називається лінія, яка має початкову точку, але немає кінцевої точки. Промінь із заданим початком, його напрямком та одиничним відрізком називається числовим променем. На наступному малюнку присутній одиничний відрізок.

Точки прийнято позначати великими літерами латинської абетки: $A,B,C$ тощо. Промені чи прямі позначають малими літерами латинської абетки: $a,b,c$ тощо. Початкову точку прийнято позначати літерою $O.$ На промені можна розташувати натуральні числа за зростанням їх значень, що можна вказати за допомогою відношення "менше" $<.$

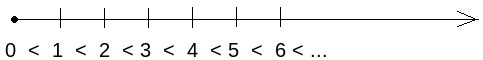
Для порівняння багатоцифрових чисел зручно користуватися наступними правилами:

1. Якщо два натуральних чисел складаються із різних кількостей цифр, то меншим (більшим) буде число із меншою (більшою) кількістю цифр. Наприклад, $5\,721<12\,123<213\,214<7\,214\,000.$

2. Якщо два натуральних числа складаються з однакової кількості цифр, то більшим (меншим) буде те число, у якого цифра у найвищому розряді більша (менша). Якщо ж цифри у найвищому розряді однакові, то порівнюються цифри наступного розряду. Наприклад, нехай дані числа $2\,451$ та $2\,476.$ У цьому випадку числові значення цифр найвищого розряду є рівними, $\color {red}{2}\,\color {black}{451}$ та $\color {red}2\,\color {black}{476}.$ Далі порівнюються числові значення цифр наступного розряду: $2\,\color {red}{4}\color {black}{51}$ та $2\,\color {red}{4}\color {black}{76}.$ Як видно, числові значення цифр у цьому випадку також рівні. Далі порівнюються числові значення цифр наступного розряду: $2\,4\color {red}{5}\color {black}{1}$ та $2\,4\color {red}{7}\color {black}{6}.$ У цьому випадку $5<7,$ і тому $2\,451<2\,476.$

Математична індукція

Якщо декотра пропозиція $\Pi$ істинна для числа $1$ та якщо з припущення, що вона є вірною для натурального числа $k,$ слідує її істинність й для числа $k+1,$ то пропозиція $\Pi$ є справедливою для будь-якого натурального числа $n\in \mathbb {N} .$ Впевнимося у цьому. Нехай $M$ - множина усіх натуральних чисел, для кожного з яких істинне висловлювння $\Pi .$ За умовою, $1\in M$ та якщо $k\in M,$ то й наступне за $k$ число $(k+1)\in M.$ Відтак за аксіомою індукції $M=\mathbb {N} .$ Відповідно, пропозиція $\Pi$ істинна для будь-якого натурального числа $n.$

Аналогічний спосіб доведення може застосованій із заміною натуральних чисел на будь-яку цілком впорядковану множину. У цьому випадку такий спосіб називається трансфінітною індукцією, суть та відмінність якого полягає у наступному. Нехай дана пропозиція $\Pi (n),$ яка формулюється для довільного натурального числа $n.$

Розгляньмо опціонал. Якщо:

• пропозиція $\Pi (1)$ є вірною;
• з того, що $\Pi (k)$ є вірною для усіх $k\leq n$ слідує, що $\Pi (n+1)$ є істинною,

то пропозиція $\Pi (n)$ є вірною для будь-якого $n\in \mathbb {N} .$

Пригадаймо, що впорядкована множина $A$ задовільняє умові мінімальності, якщо кожна її непуста підмножина містить мінімальний елемент. Якщо справджується ця умова та число мінімальних елементів довільної підмножини є скінченним, то множина $A$ називається частково впорядкованою. У випадку, якщо кожна непуста підмножина множини $A$ містить єдиний мінімальний елемент, то $A$ називається частково цілком впорядкованою. Зрозуміло, що частково впорядкована множина буде цілком впорядкованою лише за умови, якщо вона є лінійно впорядкованою.

Нехай тепер дана декотра пропозиція $\Pi (a),$ яка формулюється для кожного $a\in A,$ де $A$ - цілком впорядкована множина.

Розгляньмо наступний опціонал. Якщо:

• є вірним твердження $\Pi (a_{1}),$ де $a_{1}$ є найменшим елементом множини $A$;
• з того, що пропозиція $\Pi (a)$ є вірною для усіх $a\times b$ за $a\neq b,$ слідує, що $\Pi (b)$ є існинною,

то пропозиція $\Pi (a)$ є вірною для усіх $a\in A.$

Справді, якщо б існували елементи у множині $A,$ для яких пропозиція $\Pi (a)$ не мала б змісту, то у множині таких елементів віднайшовся б найменший, $a_{\mathrm {min} }$ (зрозуміло, що $a_{1}\times a_{\mathrm {min} }$), і ми б прийшли до суперечливості, оскільки для усіх $a\times a_{\mathrm {min} }$ за $a\neq a_{\mathrm {min} }$ пропозиція $\Pi (a)$ була б вірною в силу другої опції.

Узагальнена індукція

Нехай $A$ - впорядкована множина із умовою мінімальності та $B$ - підмножина множини $A,$ яка містить елемент $a\in A,$ якщо вона містить усі елементи $x\in A$ такі, що $x<a.$ Зрозуміло, що у випадку, якщо існують такі мінімальні елементи множини $A,$ то усі вони належать $B.$ Тоді $B=A.$ Справді, доповнення ${\bar {B}}$ у $A$ не містить мінімального елемента і тому повинне бути пустим.

Узагальнену індукцію називають нетеровою індукцією. Частковим випадком нетерової індукції є трансфінітна індукція, яка, у свою чергу, є узагальненням індукції для натуральних чисел, оскільки натуральні числа утворюють цілком впорядковану множину відносно точного відношення включення $\subseteq .$